973. Максимальная сумма на дереве

 

Дано дерево с n вершинами, где вершина с номером i (1 ≤ i ≤ n) содержит ci монет. Выберите такое подмножество вершин, чтобы никакие две из них не были смежными (то есть не соединены ребром), а сумма монет в выбранных вершинах была максимальной.

Вход. Первая строка содержит количество вершин n (1 ≤ n ≤ 105) в дереве. Каждая из следующих n – 1 строк содержит два целых числа u и v (1 ≤ u, v ≤ n), задающих ребро в дереве. Последняя строка содержит n неотрицательных целых чисел c1, ... cn – количество монет в каждой вершине дерева.

 

Выход. Выведите максимальную возможную сумму монет, которую можно получить, выбрав подмножество вершин дерева с условием отсутствия смежных вершин.

  

Пример входа 1

Пример выхода 1

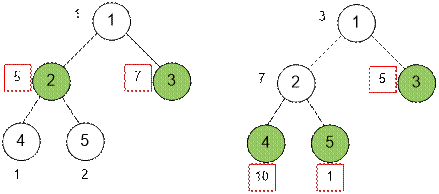
5

1 2

1 3

2 4

2 5

1 5 7 1 2

12

 

 

Пример входа 2

Пример выхода 2

5

1 2

1 3

2 4

2 5

3 7 5 10 1

16

 

 

РЕШЕНИЕ

динамичекое программирование - деревья

 

Анализ алгоритма

Пусть v – вершина дерева. Обозначим через:

·        dp1(v) наибольшую сумму монет, которую можно собрать из поддерева с корнем v, если монеты в вершине v мы берем.

·        dp2(v) наибольшую сумму монет, которую можно собрать из поддерева с корнем v, если монеты в вершине v мы не берем.

Тогда ответом на задачу будет max(dp1(1), dp2(1)), если взять первую вершину за корень дерева.

 

Определим рекурсивно приведенные функции:

·        Если монеты в вершине v мы берем, то брать монеты из ее сыновей нельзя:

dp1(v) = cv + , где to1, …, tok – сыновья вершины v.

·        Если монеты в вершине v мы не берем, то из её сыновей можно или брать, или не брать монеты. Из этих двух вариантов следует выбрать тот, в котором сумма монет максимальна: 

dp2(v) = , где to1, …, tok – сыновья вершины v.

Если v – лист дерева с cv монетами, то функции в нем примут следующие значения: dp1(v) = cv и dp2(v) = 0.

 

Пример

Расставим метки dp1(v) / dp2(v) на вершинах деревьев из примеров.

 

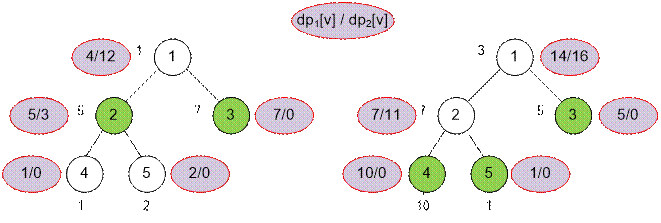
Для первого примера имеем:

·        dp1(1) = c1 + dp2(2) + dp2(3) = 1 + 3 + 0 = 4;

·        dp2(1) = max(dp1(2), dp2(2)) + max(dp1(3), dp2(3)) = 5 + 7 = 12;

·        dp1(2) = c2 + dp2(4) + dp2(5) = 5 + 0 + 0 = 5;

·        dp2(2) = max(dp1(4), dp2(4)) + max(dp1(5), dp2(5)) = 1 + 2 = 3;

 

Для второго примера имеем:

·        dp1(1) = c1 + dp2(2) + dp2(3) = 3 + 11 + 0 = 14;

·        dp2(1) = max(dp1(2), dp2(2)) + max(dp1(3), dp2(3)) = 11 + 5 = 16;

·        dp1(2) = c2 + dp2(4) + dp2(5) = 7 + 0 + 0 = 7;

·        dp2(2) = max(dp1(4), dp2(4)) + max(dp1(5), dp2(5)) = 10 + 1 = 11;

 

Упражнение

Расставьте метки dp1(v) / dp2(v) на вершинах дерева:

 

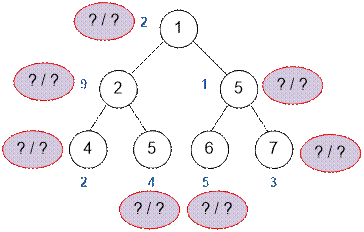
Реализация алгоритма

Объявим рабочие массивы.

 

vector<vector<int> > g;

vector<int> dp1, dp2, cost;

 

Функция dfs реализует поиск в глубину. Вычисляем значения dp1 и dp2 во всех вершинах дерева.

 

void dfs(int v, int p = -1)

{

  dp1[v] = cost[v];

  dp2[v] = 0;

 

  for (int to : g[v])

  {

    if (to == p) continue;

 

    dfs(to, v);

 

    dp1[v] += dp2[to];

    dp2[v] += max(dp1[to], dp2[to]);

  }

}

 

Основная часть программы. Читаем дерево и массив монет.

 

scanf("%d",&n);

g.resize(n+1);

for(i = 1; i < n; i++)

{

  scanf("%d %d",&u,&v);

  g[u].push_back(v);

  g[v].push_back(u);

}

 

dp1.resize(n+1); dp2.resize(n+1);

cost.resize(n+1);

for(i = 1; i <= n; i++)

  scanf("%d",&cost[i]);

 

Пусть корень дерева находится в вершине 1. Запускаем из нее поиск в глубину.

 

dfs(1);

 

Вычисляем и выводим ответ.

 

ans = max(dp1[1], dp2[1]);

printf("%d\n",ans);